Hessian Matrix ( 헤시안 행렬 )

매직블럭 2013. 6. 21. 17:46

주어진 제약 조건 하에서 목적함수를 최적화하는 라그랑지함수의 2계조건이라 볼 수 있다.

헤시안 행렬 H gamma > 0 이면, 일계함수 라그랑지를 만족시키는 근에서 극대이며,

헤시안 행렬 H gamma < 0 이면, 일계함수 라그랑지를 만족시키는 근에서 극소이다.

즉 Boardered hessian은,

주어진 목적함수 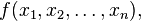$f(x_1, x_2, dots, x_n),$ 에 대하여 헤시안 행렬은

$H(f) = \begin{bmatrix} \frac{\partial^{2} f}{\partial x_{1}^2} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^2} & \cdots & \vdots \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \cdots & \cdots & \frac{\partial^{2} f}{\partial x_{n}^2} \end{bmatrix}$

다음과 같이 계산..

헤시안 행렬은, 함수의 기울기벡터 $\nabla f$ 에 대한 야코비 행렬로도 설명이 가능하다

뭐 정리하자면 어떤 함수에 대하여 이계도함수들을 행렬화 시켜놓은것이 헤시안 메트릭스

각 원소의 규칙은 위의 것과 같고 이계도함수 값으로 구성되어 있어서 극값 판명에 사용이 가능하다는점

surf 검색하다 뭔가 궁금해서 찾아보는데., 이것도 모르겠다 ㅋ 당최 아는게 없네

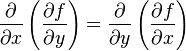
특정 함수가 두번 미분이 가능하고, 미분된 함수가 연속이다 라는 조건을 붙이게 되면 위 식이 성립하게 된다.

그래서 헤시안 메트릭스를 구성하게 되면 대칭행렬의 형태로 나타나게 된다.

[출처] Hessian Matrix|작성자 프란츠

저작자표시 비영리 (새창열림)