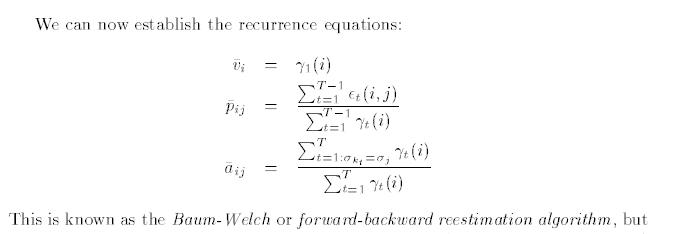영상을 이용하다 보면 조명에 의한 영향력을 제거 하고 싶은 경우가 꽤나 빈번하게 발생한다.
근사화에 대한 내용을 보다 보니 언젠가 쓸수도 있겠다 싶은 내용이 있어서 기록.
=============================================================
위 영상과 같은 경우는 조명이 다양하지 않고 한쪽 방향에서만 가해지는 단순한 형태이다.
영상의 형태에 대한 곡면의 방정식을 구하고 이 방정식의 파라미터를 근사화 하면
조명에 의한 배경을 근사화 할 수 있다
이와같은 곡면에 대한 방정식은 일반적으로 아래와 같다.
임의의 좌표를 샘플링 해서 아래와 같이 방정식의 파라미터를 계산하는 과정이 필요하다.
앞의 x, y 로 구성된 행렬의 역핼렬을 구해 좌우변에 곱해주면 원하는 파라미터를 구할 수 있다.
이제 방정식이 완성 되었으니 식을 이용하여 좌표값을 대입하면 전체 영상에 대한 조명배경을 구할 수 있다.
배경을 구했으니 전경과의 차를 이용하여 원하는 내용만을 남길 수 있겠지.
물론 실제 어플리케이션에서는 다른 다양한 작업들이 추가 되어야만 사용 가능 할 것이다.
이러한 배경제거를 이용하면 이진화 연산에도 도움을 얻을 수 있다.
원 영상을 일반적인 하나의 임계값으로 이진화 할 경우는 올바른 이진화가 안 될 가능성이 높다.
하나의 임계값을 통해 두개의 영역으로 나뉘는 경우는 일반적으로 별로 없기 때문이다.
아래의 영상과 같이 정보가 날아가는 경우를 확인 할 수 있다.
이런 경우 보다 깔끔한 이진화 결과를 얻을 수 있다.
위의 모든 내용이 출처에 보다 자세히 설명 되어 있음.
원본 그림을 제외한 나머지 영상은 확인을 위해 본인이 계산하여 얻은 결과물임.
원본 그림 출처 : http://darkpgmr.tistory.com/56
'전공관련 > Algorithm' 카테고리의 다른 글
| Bagging vs Boosting 비슷한듯 비슷하지 않은 개념. (3) | 2014.12.24 |
|---|---|
| Local Patch Descriptor - Ferns Feature (0) | 2014.11.20 |
| 주성분분석 ( Principal Component Analysis ) - PCA (0) | 2014.09.17 |
| K-Mean Clustering (0) | 2013.08.13 |
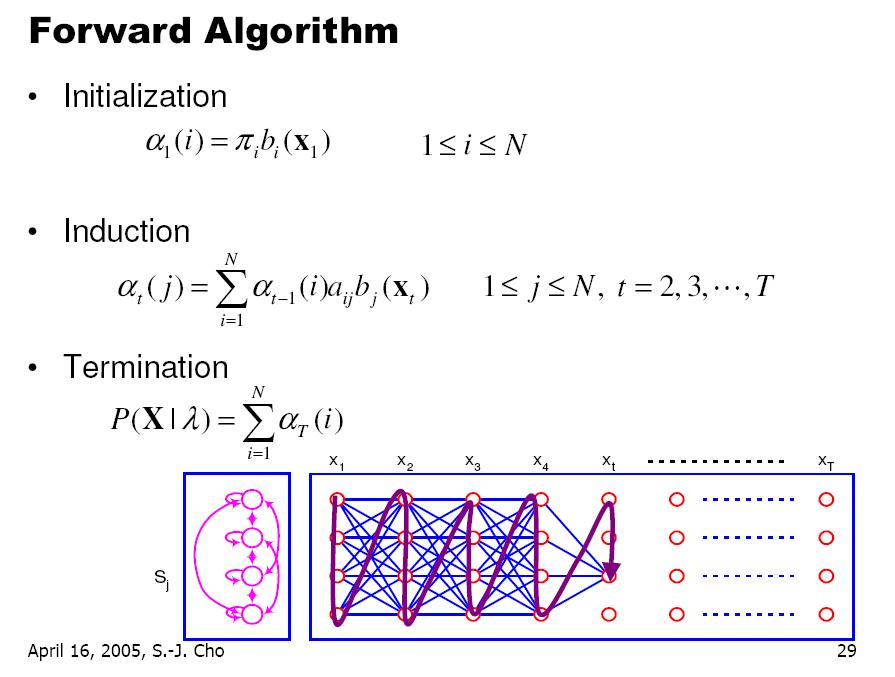
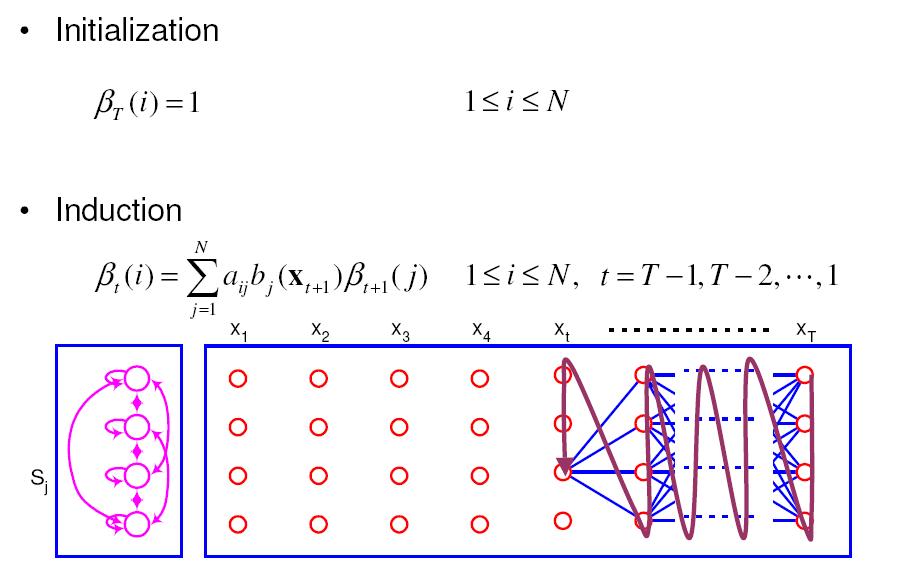
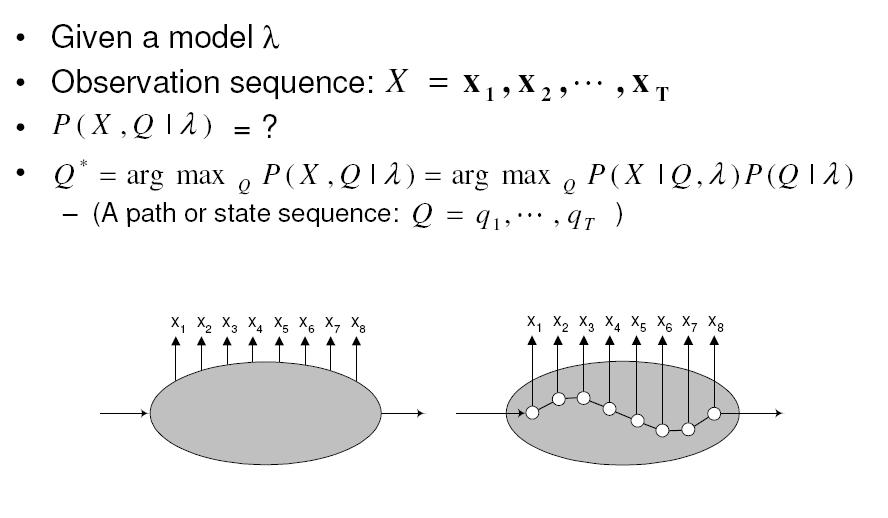
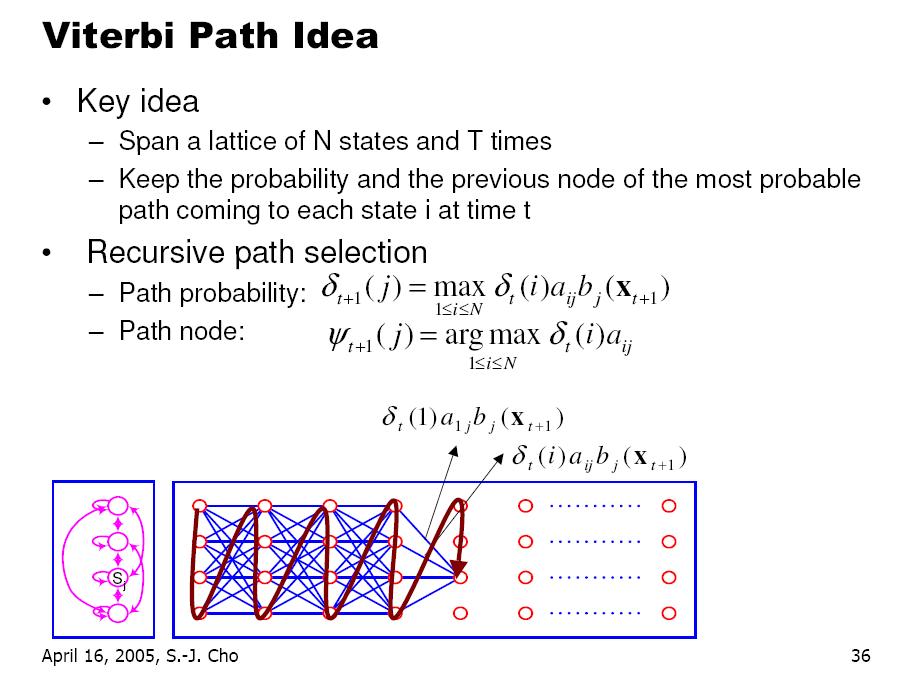
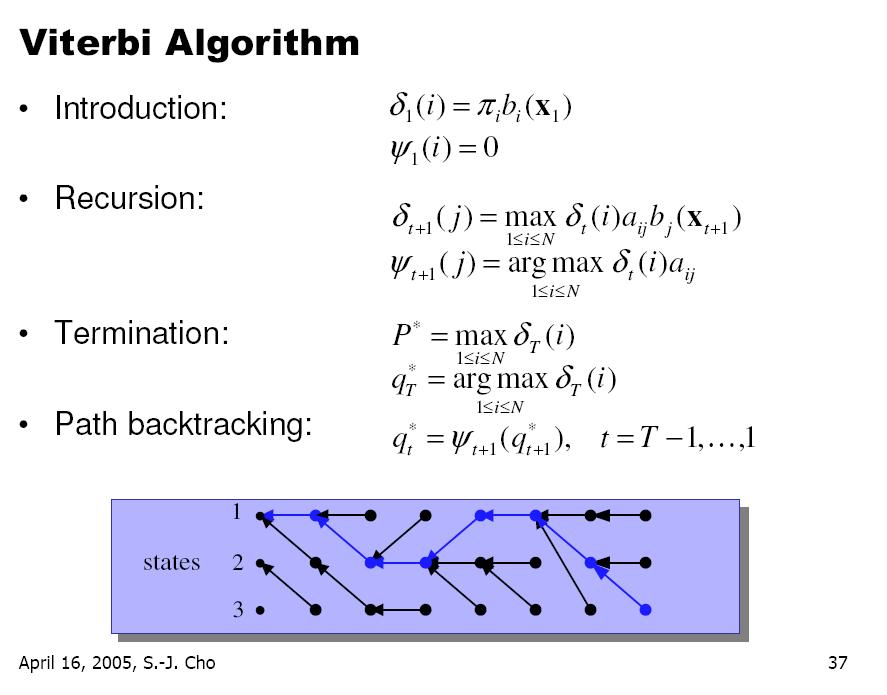
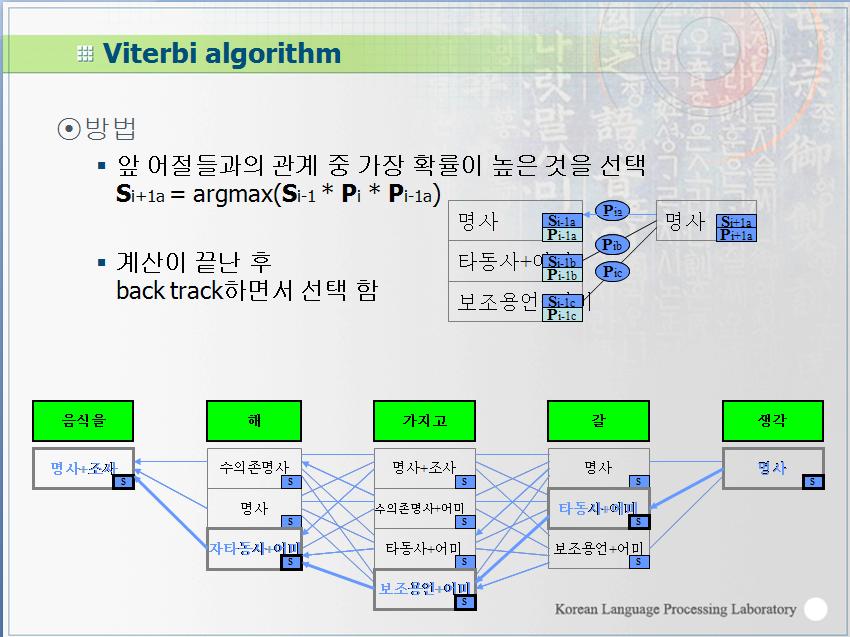
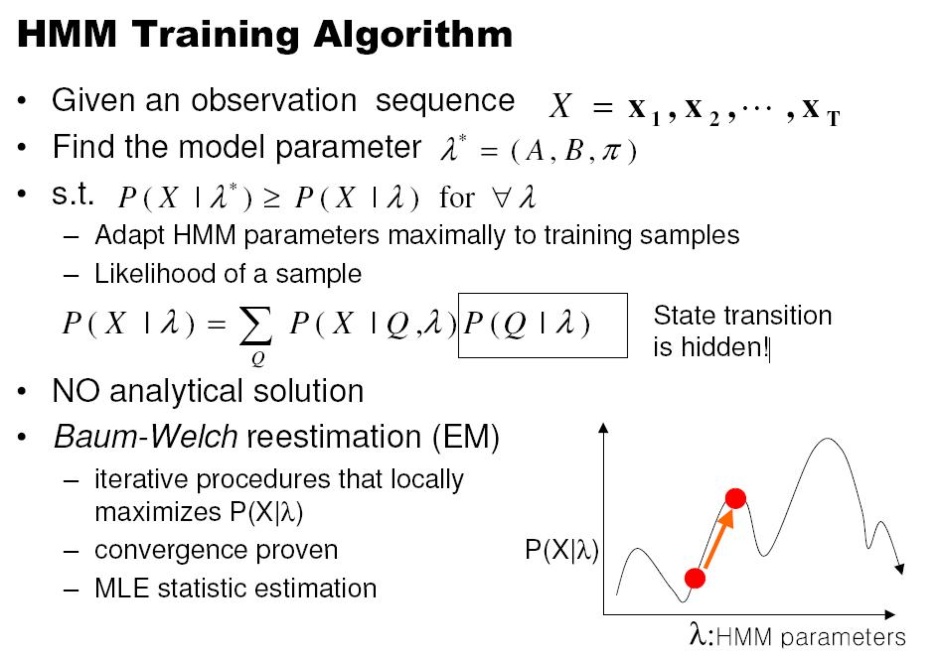
| Hidden Markov Model ( HMM ) (0) | 2013.08.06 |